高斯过程的理论与公式实在难以看懂，打算先把它晾在一边，先假设我已经可以成熟运用（当然如果仅仅是应用，scikit-learn 调用一下就可以），看看高斯过程能用来做什么。主动学习就是一个非常好的选择。想象下这么个场景，现在可以买到的化合物库可能达到了一个亿，如果将每个化合物都去进行分子对接，一个化合物如果需要 10 秒的计算时间，即使有 1 万个核，也需要 12 天的时间，再想想 10 亿秒的 CPU 时间需要多少钱，就劝退所有学术界了。使用机器学习模型预测小分子结合亲和力（又叫打分函数）就会快很多，所以我们可以挑几万个分子出来对接，然后建个模型以预测所有化合物。速度会快很多，但应该怎么挑呢？所谓主动学习就是，根据现有的模型，挑选下一批更合适的样本作为训练机来提高模型的预测能力。

且慢，我们再思考下我们的目的是什么，是为了得到很好的机器学习模型预测打分函数吗？不是，我们的目的仅仅是找到最合适的化合物，即得打分函数的最大值（所对应的化合物）。所以我们就可以用贝叶斯优化来得到最合适的化合物。对于最优化问题，经常会提到一个概念，后续也会再次提到，那就是权衡探索（explore）和挖掘（exploit）。很好理解，当我们得到一个结合亲和力很不错的小分子后，我们应该在这个小分子的基础上进行微调，从而挖掘出（局部）最优的结构，还是应该尽可能多的探索整个化学空间以得到更多样的分子呢，答案一定是介于俩者之间，既需要利用已知的高活性化合物，又不能让自己陷入局部最优。

介绍算法前先提两个术语：

代理模型 (Surrogate Function)： 也就是上面提到的机器学习模型，从名字也能看出来，它的作用就是作为分子对接的代理。叫模型也好，叫函数也罢，总之就是给定一个新化合物，它能告诉你其结合亲和力以及“预测把握”。这个“把握”很重要，就像学生在平时做卷子时，我们并非只想知道他到底对还是不对，而是希望知道他是会还是不会，从中知道哪些知识点欠缺。同样，贝叶斯优化的过程中，代理模型的作用并非真的去预测结合亲和力，而是提供预测概率，这样才能知道它有没有可能是潜在的药物。

采集函数 (Acquisition Function)：顾名思义，这个函数的目的是确定下一次要选择那些样本进行训练。函数会返回最佳的采集样本，选择完后，这些样本会和之前的训练集放在一起生成一个新的代理模型。

整个贝叶斯优化的过程其实很简单，可以认为是下面四个步骤的循环：

  1. 随机选择些候选样本（如果计算所有可能代价过大）
  2. 用采集函数计算这些样本的打分并选出最优的 x
  3. 计算该样本的真实值 actual
  4. 将新的训练样本和之前的放在一起得到新的代理模型

可以用如下代码表示（例子中数据为 1 维）:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 省略初始化
for i in range(100):
    # 选择候选样本
    Xsamples = random(100).reshape(len(Xsamples), 1)
    # 打分
    scores = acquisition(X, Xsamples, model)
    # 根据选择最终样本
    ix = argmax(scores)
    x = Xsamples[ix, 0]
    # 获得真实值
    actual = objectve(x)
    # 更新模型
    X = vstack((X, [[x]])
    y = vstack((y, [[actual]])))
    model.fit(X, y)

稍微补充一句，这里采集的过程是每次随机选择 100 个样本进行打分，但实际用的时候一般会采用一些最优化算法，毕竟我们的目的就是得到 acquisition 最高的样本，因此可以用最优化的算法进行采样。比如可以用：

1
2
3
4
5
6
7
8
9
10
from scipy.optimize import minimize
def min_obj(Xsamples):
  return -acquisition(X, Xsamples, model)
min_val = 0
x = None
for i in random(100).reshape(len(Xsamples),1):
  res = minimize(min_job, x0=i)
  if res.fun < min_val:
    min_val = res.fun[0]
    x = res.x

采集函数

采集函数可能算是贝叶斯优化的核心，毕竟它决定了我们该如何选择下一个要学习的样本。这里介绍两个算法，最容易理解的 PI 法 和最常见的 EI 法。

  • Probability of Improvement (PI)
  • Expected Improvement (EI)

Probability of Improvement (PI)

PI 法的公示如下：

$$ x_{t+1} = argmax(\alpha_{PI}(x)) = argmax(P(f(x))\geqslant (f(x^{+}+\epsilon))) $$

即找到一个位置 $x_{t+1}$, 要求该位置下的函数值 f(x) 比已知最大值 $f(x^+)$ 还要大 $\epsilon$ 的概率最高。怎么理解“比他大的概率”？如果代理模型用的是高斯过程就不难理解了，因为在这个模型下，每个预测值都是一个正态分布。举个例子：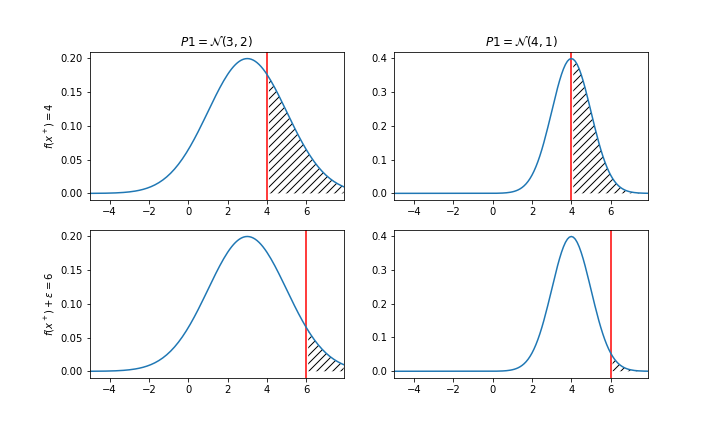
BO-PI.png

上图分别对应两个潜在样本，或者叫位置 P1 和 P2，P1 的预测均值为 3、方差为 2， P2 的预测均值为 4，方差为 1。假设已知代理模型的最大值是 4，那我应该考虑下次计算 P1 还是 P2 呢？如果不考虑 $\epsilon$，那么似乎 P2 更好，P2 比 4 大的概率为 50%（曲面下面积），而 P1 肯定是不到 50%。毕竟 P2 均值就是 4，显然更有竞争力。不过一个冒险家可能更喜欢 P1，就是因为 P1 有更大的不确定性，如果将我的期望提高到 6，即看上图的下面两张图，不难发现此时 P1 的概率就高过了 P2。我们用公式让它描述的更具体一点：

$$ x_{t+1} = argmax \Phi(\frac{\mu_t(x)-f(x^+)-\epsilon}{\sigma_t(x)}) $$

其中$\Phi$是标准正态分布的累积分布函数，该公式的意思就是计算图中阴影处的面积，并选择最大的那个情况。$\epsilon$ 就是一个权衡探索和挖掘的参数，该值更高，意味着我想探索更高的可能，如果它方差很大的话，我能容忍更低的均值。上图仅仅描述了两个点的比较，下面这张图可能能更好地理解在采集函数和 y 以及 x 的关系。该图中已知最大值是第三个点，在此基础上增加个 $\epsilon$ 便是橙色的线，然后就看所有 x 下，哪个点的粉色部分概率面积最大，也就是 6 这个点。

用代码描述：

1
2
3
4
5
6
7
8
9
10
11
def acquisition(X, Xsamples, model, e):
  # Xsamples 是候选样本， X 是训练集
  # 计算目前最大值
  yhat, std = surrogate(model, X)
  best = max(yhat) + e
  # 计算候选样本的均值和标准差
  mu, std = surrogate(model, Xsamples)
  mu = mu[:, 0]
  # 计算这些样本高于最大值的概率
  probs = norm.cdf((mu - best) / (std+1E-9))
  return probs

Expected Improvement (EI)

EI 法稍微复杂一点，相对于 PI 只关心其比已知最大值还大的概率， EI 关心的是比已知最大值大多少，即求两者差的数学期望。

$$ EI(x) = \mathbb{E} max(f(x)-f(x^+), 0) $$

从中可以看计算 EI 时不关心比已知最大值小的概率（如果考虑它，直接计算平均数就是了）公示不详细推导了，可以参考这个，下面仅仅考虑没有 $\epsilon$ 的情况。公示中用 $\mu, \sigma$ 表示 f(x) 的均值和方差，$f^*$ 表示最大值。

$$ EI(x) = \int_{-\infty}^{(\mu-f^*)/\sigma}(\mu-f^*-\sigma\epsilon)\phi(\epsilon)d\epsilon \\ = (\mu-f^*)\Phi(\frac{\mu-f^*}{\sigma})-\sigma\int_{-\infty}^{(\mu-f^*)/\sigma}\epsilon\phi(\epsilon)d\epsilon \\ = (\mu-f^*)\Phi(\frac{\mu-f^*}{\sigma}) + \sigma\phi(\frac{\mu-f^*}{\sigma}) $$

笔者对此的理解就是在原来的概率基础上乘以“增量”，即可以认为是从曲面面积变成了高为 $y-f^*$ 的体积。

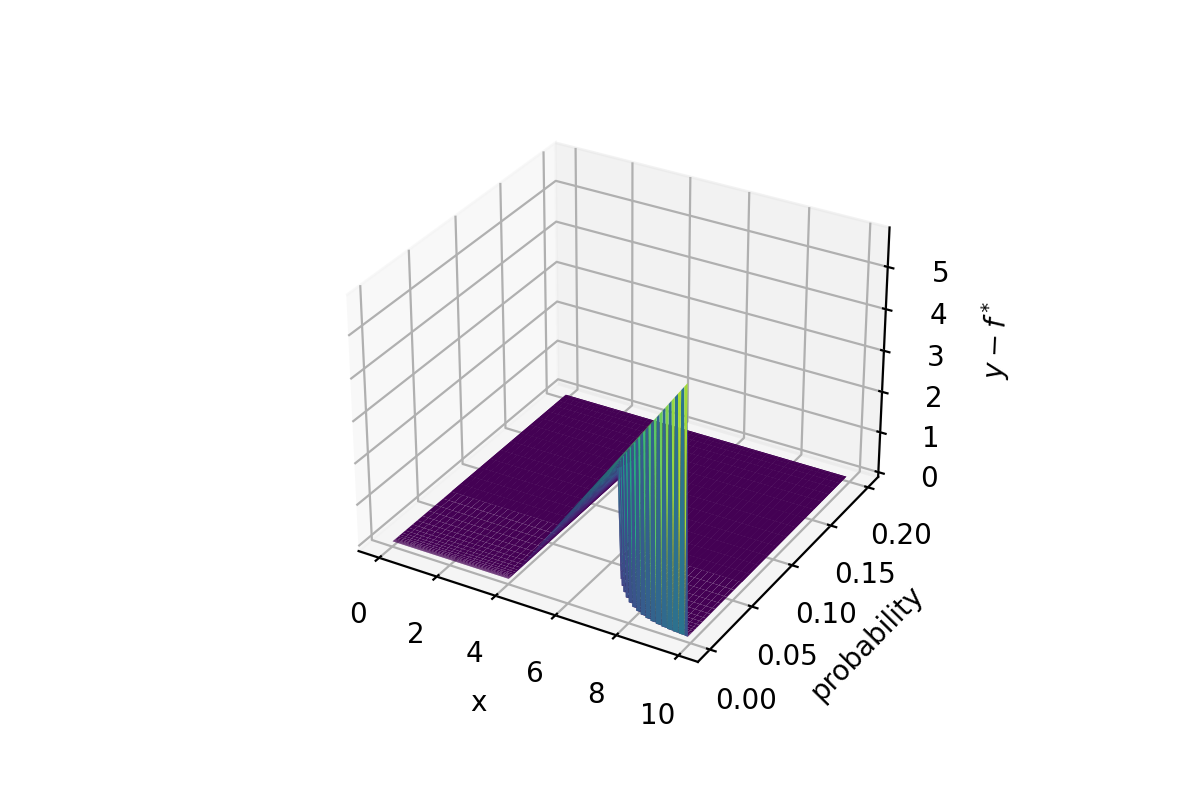
BO-EI.png

和 PI 一样，如果要增加“探索系数”，在原来 $\mu-f^*$ 的基础上再减去一个 $\epsilon$，当然注意这个 $\epsilon$ 和上述公示里的不是同一个，公式里的可以理解为是一个随机变量的微分，而非一个参数。

用代码可以这样描述:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def acquisition(X, Xsamples, model, e):
  # Xsamples 是候选样本， X 是训练集 和 PI 部分一样
  yhat, std = surrogate(model, X)
  best = max(yhat) + e
  mu, std = surrogate(model, Xsamples)
  mu = mu[:, 0]

  with np.errstate(divide='warn'):
      imp = mu - best
      Z = imp / std
      ei = imp * norm.cdf(Z) + std * norm.pdf(Z)
      ei[std == 0.0] = 0.0  # 已知的点不考虑

  return ei

代理模型的选择

在大多数贝叶斯优化的介绍里，代理函数一般都选用高斯过程，该方法和贝叶斯优化可谓黄金搭档，高斯过程不仅能提供点估计，还能给出预测分布。这样就可以利用预测的高斯分布来进行贝叶斯优化。可高斯过程也有个缺点，那就是训练速度太慢，而且随样本数量增加呈立方增长，比如如果样本从 100 增加到 1000 训练需要额外增加 1 秒，那就意味着样本数达到 10000 需要增加 1000 秒，而样本数达到十万后，训练时间将达到 12 天。按这个速度建模，用“代理模型”倒还不如直接用分子对接进行预测来的快，又需要什么贝叶斯优化。所以贝叶斯优化更多可能还是用在计算样本量小但采样成本相对较大的情况，比如机器学习模型的超参优化。如果硬要使用代理模型处理最开始提到的场景，即希望训练成千上万化合物的打分函数，那么最好是采用一些其他技术得到预测概率，比如可以用贝叶斯神经网络，或者用其他校准方式以得到预测的“不确定性”。

实现

如果用 scikit-learn 建模要做超参优化的话，推荐用 scikit-optimize。
https://scikit-optimize.github.io/stable/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from skopt import BayesSearchCV
from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split

X, y = load_digits(n_class=10, return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, test_size=.25, random_state=0)

# log-uniform: understand as search over p = exp(x) by varying x
opt = BayesSearchCV(
    SVC(),
    {
        'C': (1e-6, 1e+6, 'log-uniform'),
        'gamma': (1e-6, 1e+1, 'log-uniform'),
        'degree': (1, 8),  # integer valued parameter
        'kernel': ['linear', 'poly', 'rbf'],  # categorical parameter
    },
    n_iter=32,
    cv=3
)

opt.fit(X_train, y_train)

print("val. score: %s" % opt.best_score_)
print("test score: %s" % opt.score(X_test, y_test))

其他的工具包括：

参考资料