高斯过程笔记 1 - 关于贝叶斯统计中的基本概念理解
Comment如果问统计学模型和机器学习模型有什么交集,那么高斯过程作为一个兼具理论与实际应用的算法自然首当其冲。直接百度下高斯过程自然能看到许多通俗的解释,比如:
高斯过程指的是一组随机变量的集合,这个集合里面的任意有限个随机变量都服从联合正态分布 (百度百科)
高斯过程被认为是一种机器学习算法,是以惰性学习方式,利用点与点之间同质性的度量作为核函数,以从输入的训练数据预测未知点的值。其预测结果不仅包含该点的值,而同时包含不确定性的资料-它的一维高斯分布 (维基百科)
前者描述其数学本质,后者描述其应用价值,虽然都描述的很到位,但似乎仍然不知其所云。于是我尝试去读读相关的书籍,比如 Gaussian Processes for Machine Learning,读了一会发现仍然不知其所云。心想还是一步一步从简单的统计学理论开始学起。
高斯过程是什么
(这是我自己的理解,如果有错误还请指正!)
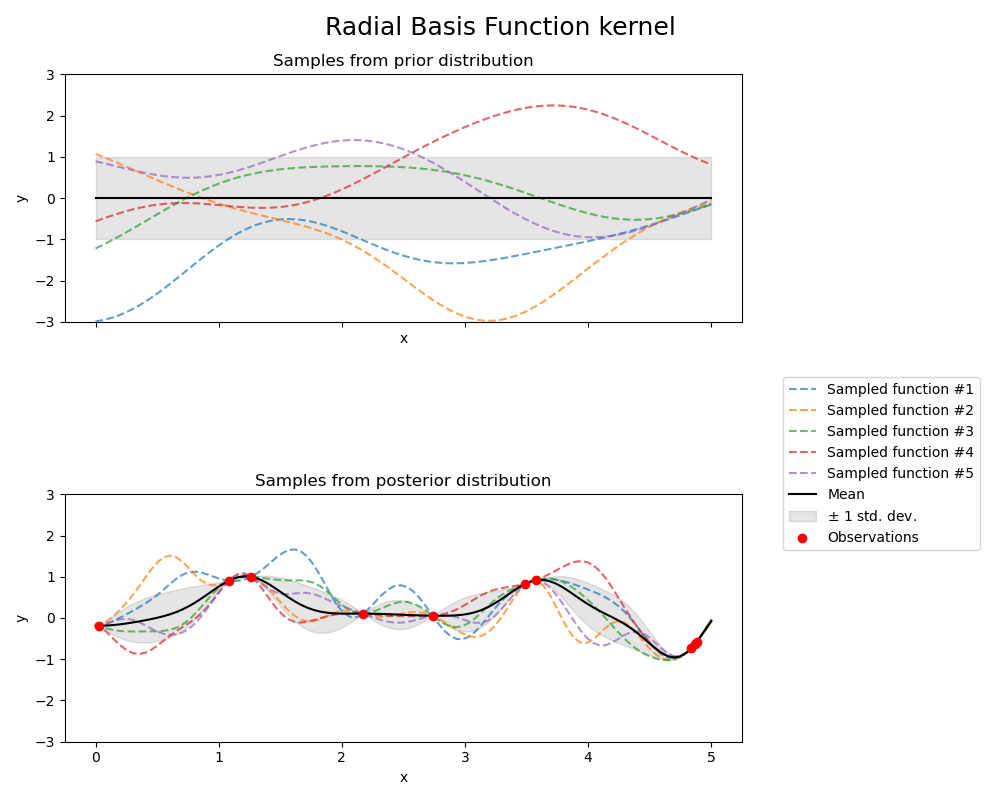
先强行逼自己相信高斯过程就是 “无数函数(f)”,这些无数的 f 满足正太分布,如图 1 上所示,里面有无数条曲线(每个曲线都是一个函数),对于一个特定的 x 值,这些曲线的 f(x) 值均值为 0 方差为 1。我们称 p(f) 之为先验分布。
当我们知道 X, y 之后,f 的分布发生变化,p(f|X, y) 就称之为后验分布。再次强迫自己相信,当 X, y 即训练集已知时,这些无数的函数就一定经过 X, y(f 在这 x0 点上是均值为 y0, 方差为 0 的正态分布)。
贝叶斯统计的基本概念
虽然说不去理解贝叶斯的公式也能硬记高斯过程,但有时候会有些茫然,
所谓先验分布、后验分布、似然(likelihood)和边界似然(marginal likelihood)到底是什么?
$$ p(x, w) = p(x|w)p(w) = p(w|x)p(x) $$
但看公式很容易理解,就是联合概率等于条件 A 下发生的概率乘以条件 A 本身发生的概率。然而考虑到该公式的具体应用便有了“先验分布”、“后验分布”,“似然”与“边际似然“这四个术语。数学上说 x 和 w 可以互换,所以我之前一直纳闷为什么 p(w) 是先验概率而 p(x) 就是边界似然呢,边界似然到底又是什么。
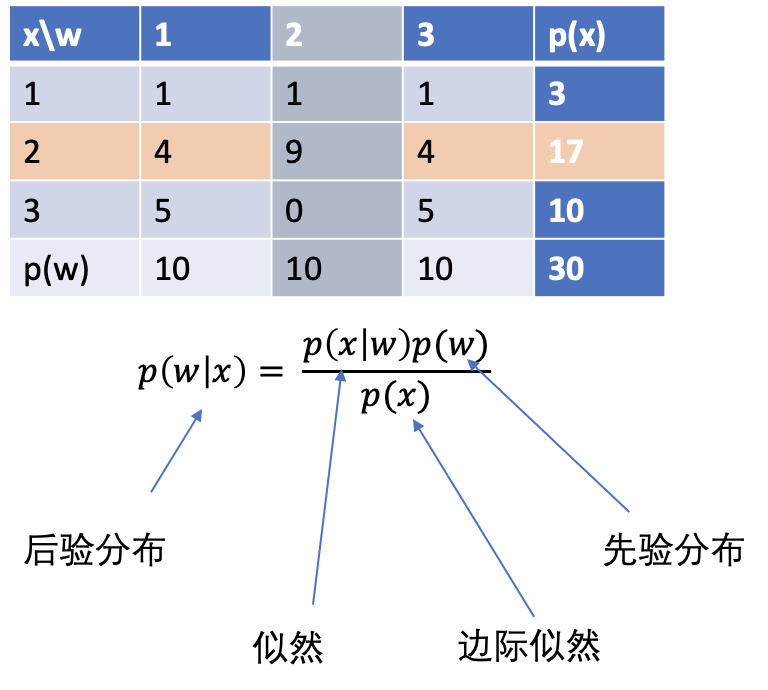
从图中我们可以看到 w = 1,2,3, x = 1,2,3 时他们发生的概率 p(w,x) 即表格上的值除以 30(总发生频次)。x 即观测值或者叫条件,从上帝视角看,x 有 3 种可能,但现实生活中我们只观测一次,比如建机器学习模型,训练集 X, y 就是观测值,虽然有无数可能的训练集,但实际应用(即建一次模型)中我们只有一个训练集。所以第二行才是我们关心的。对于参数模型,如线性回归,我们想要得到最佳参数 w 使得其和训练集最吻合,而从贝叶斯统计的角度,我们想要知道 p(w|x),即已知训练集的条件下,不同 w 的概率是多少。从上帝视角看分别是 4/30, 9/30 和 4/17,(若我们使用极大似然估计,则最后 w = 2)。
竖着看,不同 w 下 x 发生概率叫做 likelihood,我称之为可能性,这往往比较容易得到;比如 w 是抛硬币的次数(往往是我们需要估计的参数),那么我们不难算出不同观测值(正面朝上)发生的概率,因为它满足二项式分布。而 p(x) 则就是所有条件 w 下 x 发生的总概率,在表格里就是 17/30,故而叫边际似然,想象下这是写在这个表的边上一个数字。
横着看,在我们不知道观测值时,我们假设所有可能的情况下 w 发生的概率叫做先验概率,其分布自然叫先验分布(即最后一行),而已经观察到 x=2 时 不同 w 下发生的概率叫后验概率(即第二行)。
贝叶斯公式虽然也可以倒着看(类似将这张表转置),但这些术语其实更多的是对应应用场景:p(w|x) 是观测到 x 时,估计参数 w 的概率,叫后验概率,对应的没有观测之前 p(w) 叫先验概率。而对调下,p(x|w) 指的是已经知道参数是 w 时,观测到 x 的可能性叫 likelihood(往往是能可计算的),所有参数情况下,x 发生的总和叫做边际似然。
回过头看这张表再去理解贝叶斯公式,每列的分布叫 likelihood,往往是已知的,比如高斯过程则是假设所有过程满足高斯分布。但我们想知道的是第二行参数 w 的分布;无法直接知道,则可以通过假定一个先验分布(最后一行)推测后验分布(第二行),推测过程中一个重要的因素就是要求边际分布,理论上说很简单,既然我们知道任意 w 下 x 的分布,对 w 做积分即可,但实际计算起来并非易事,所以才需要用一些近似的方法